Class 10 Physics Chapter 10 Light : Reflection and Refraction

 ~ Image Formation in Lenses Using Ray Diagrams 

We can represent image formation by lenses using Ray diagrams. Read diagrams will also help us to study the nature, position and relative size of the image formed by lenses. For drawing Ray diagrams in lenses, a like of spherical mirrors, we consider any two of the following rays - 

i) A ray of light from the object, parallel to the principal axis, after refraction from a convex lens coma passes through the principal focus on the other side of the lens, as shown in figure. 10.13 (a). 

                                           Fig 10.13 (a)

In case of a convex lens, the ray appears to diverge from the principal focus located on the same side of the lens, as shown in fig. 10.13 (b).    

                                                 Fig 10.13 (b) 
  

ii)  A ray of light passing through a principal focus, after refraction from a convex lens, will emerge parallel to the principal axis. This is shown in fig. 10.14 (a). 

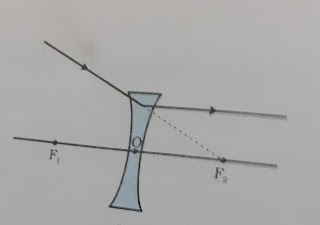
                                             Fig 10.14 (a) 

A Ray of light appearing to meet at the principal focus of a concave lens coma after refraction, I will emerge parallel to the principal axis. This is shown in fig. 10.14 (b).

                          Fig 10.14 (b)

 iii) A ray of light passing through the optical centre of a lens will emerge without any deviation. This is illustrated in fig.10.15 (a) and fig.10.15 (b). 

The ray diagrams for the image formation in a convex lens for a few positions of the object are shown in Fig. 10.16. 

Direct diagrams representing the image formation in a concave lens for various positions of the objects are shown in Fig. 10.17.    

  

 

~ Sign Convention for spherical Lenses 

For lenses, we follow sign conventions, similar to the one used for spherical mirrors. We apply the rules for signs of distances, except that all measurements are taken from the optical centre of the lens. According to the convention, the focal length of a convex lens is positive and that of a concave lens is negative. You must take care to apply appropriate signs for the values of u, v, f, object height h and image height h' .

~POWER OF A LENS 

you have only deal and leather every the opulence to convert john i watch live is depends on its focal length . For example , a convex lens of short focal length bends the light rays through large angles, by focusing them closer to the optical Centre. Similarly, concave lens of very short focal length causes higher divergence then the one with the longer focal length. The degree of convergence or divergence of light  rays  achieved  by a lens is expressed in terms of its power. The power of a lens is defined as the reciprocal of its focal length. It is represented  by the letter P. The power P of a lens of focal length f  is given by 

 

The SI unit of power of a lens is 'dioptre'. Iit is denoted by the letter D. If expressed in dioptres. Thus, 1 dioptre is the power of a lens whose focal length is 1 metre. ID = 1m/-1. You may note that the power of a convex lens is positive and that of a  concave lens is negative. 

Opticians prescribe corrective lenses indicating their powers. Let us say the lens prescribed has power equal to + 2.0 D. This means the lens prescribed is convex. The focal length of the lens is +0.50 m. Similarly, a lens of power - 2.5 D has a focal length of - 0.40 m. The lens is concave.